Взаимосвязь характеристических свойств функций выбора

План лекции №6

1. Основные утверждения о комбинировании свойств функций выбора
2. Связь свойства константантности со свойствами наследования, согласия и отбрасывания в общем случае
3. Свойства согласия, наследования, отбрасывания и константантности для функций одиночного выбора
4. Связь принципа Кондорсе со свойствами наследования и согласия
5. Связь условий Кондорсе со свойствами наследования и согласия для функций одиночного выбора
6. Значение принципа Кондорсе в классической теории принятия решений и понятие нормальных функций выбора

Классы функций выбора:
К1. Произвольные
К2. Функции непустого выбора
К3. Функции одиночного выбора

1. Для функций выбора классов К1 и К2 свойства наследования, согласия и отбрасывания никак не связаны!

2. Для функций одиночного выбора (из К3) свойство согласия является более общим чем свойства наследования и отбрасывания , которые эквивалентны.

Примеры комбинирования свойств для функций непустого выбора

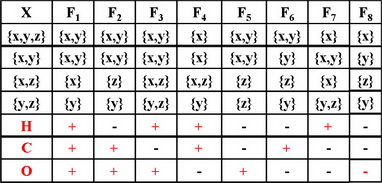
Эти примеры доказывают утверждение 1.

Доказательство утверждения 2

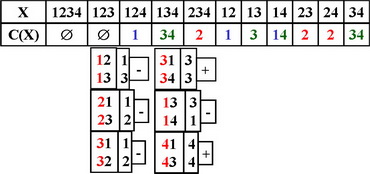
Одноэлементные функции     C(X¹) ⊇ C(X) /\ X¹     C(X²) = C(X)

1. При проверке свойств Н и О совпадает порядок формирования анализируемых предъявлений (от обобщающего предъявления – к частичным)

2. Для функций одиночного выбора частичные предъявления, формируемые для проверки свойств Н и О, - совпадают.

3. По содержанию проверок условия отбрасывания являются достаточными для условий наследования (равенство множеств является достаточным для включения одного в другое).

4. Включение одноэлементного множества в другое одноэлементное множество означает их совпадение (все множества C(X) содержат в точности по одному элементу).

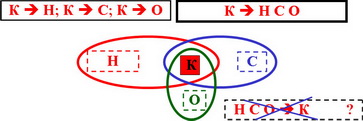
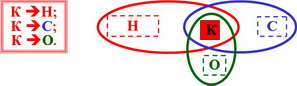
1. Для произвольной функции выбора C( ) из выполнения свойства константантности К следует выполнение свойства наследования Н: ( К → Н )

2. Для произвольной функции выбора: ( К → О )

3. Для произвольной функции выбора: ( К → С )

Иллюстрация взаимосвязи свойств Н, С, О и К в общем случае

Пример, когда свойства НСО выполняются, а свойство К не выполняется (выбор не пуст):

К → Н С О , (как и в общем случае)
Н С О → К ?     Н С О = К ?     Н = К ?     Н → К ?     С → К ?     О → К ?

Функция C(X) – одноэлементная, кроме того проверяемое частичное предъявление X¹ должно содержать в себе выбранный вариант, поэтому знак ⊇ эквивалентен знаку =. Поэтому     Н → К     т.е.     Н = К

Так как C(X) содержит один элемент, то частичные предъявления X² не отличаются от частичных предъявлений, проверяемых в свойстве К, а так как совпадают и сами проверяемые условия, то :     О → К     т.е.     О = К     т.е.     Н = О = К

Пример функции одноэлементного выбора С(Х) :

Свойство С выполняется, а Н=О=К - нет !

Иллюстрация взаимосвязи свойств Н, С, О и К для функций одиночного выбора

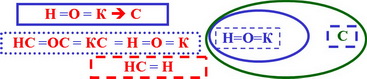
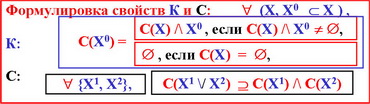
Иллюстрация взаимосвязи свойств Н, С, О и К для функций непустого выбора

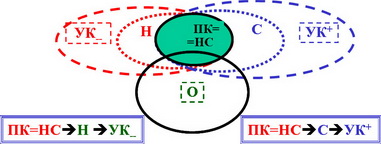
ЕСЛИ выполняется принцип Кондорсе, ТО выполняются свойства согласия и наследования, и НАОБОРОТ, ЕСЛИ выполнены оба свойства : и наследования, и согласия, ТО выполняется и принцип Кондорсе.

1. ПК → Н,С;     2. Н,С → ПК;     3. НС = ПК

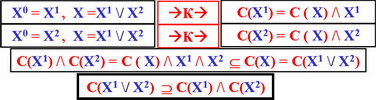
Доказательство второй связи 2. Н,С → ПК;

С → УК⁺     Н → УК_-     (из определений УК)

Н,С → УК⁺,УК_- = ПК

Доказательство первой связи ПК → Н,С

Что известно:     С → УК⁺     Н → УК_-     (из определений УК)
ПК → УК⁺     ПК → УК_-     (из определений ПК)
Докажем, что: ПК → С
Пусть x ∈ С(X1) /\ С(X2)    
из x ∈ X1 и УК- : x ∈ C(x,y1), y1 ∈ X1    
из x ∈ X2 и УК- : x ∈ C(x,y2), y2 ∈ X2
x ∈ C(x,y), y ∈ X1 \/ X2
Используем УК+ : x ∈ C(X1 \/ X2), т.е. свойство С – вып!
Докажем, что: ПК → Н
Пусть x ∈ C(X)
Используем УК- : x ∈ C(x,y), y ∈ X, и для y ∈ X1 ⊂ X
Используем УК+ : x ∈ C(X1) , т.е. свойство Н – вып!

Иллюстрация связей условий Кондорсе и свойств Н, С, О в общем случае

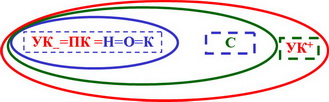
Таким образом, если выполняется принцип Кондорсе, то выполняются свойства согласия и наследования, и наоборот, если выполнены оба свойства : и наследования, и согласия, то выполняется и принцип Кондорсе.

Известно:

Н=ПК=НС ? → УК-
? Проверим усиление (=,←):
Н ← УК- ?     УК- → Н ?
Проверим Н, используя УК-
Пусть x ∈ C(X), тогда x =C(x,y), где y ∈ X.(∀y)
Пусть z ≠ x, z ∈ X1 ⊂ X), тогда z ≠ C(X1), т.к. z ≠ C(x,z ).
т.е C(X1) = x. Следовательно, свойство Н –выполнено!

Иллюстрация связей условий Кондорсе и свойств Н, С, О для функций одиночного выбора

Пример, когда свойство УК+ выполняется. а свойство С - не выполняется:

Функции выбора, удовлетворяющие принципу Кондорсе, называются нормальными.

Выполнение принципа Кондорсе эквивалентно одновременному выполнению свойств наследования и согласия. Функции с подобными свойствами исследуются в классической теории принятия решений.

Если выполняется принцип Кондорсе, то функция выбора однозначно определяется своими значениями для двух- и одноэлементных предъявлений.

Вычисление классической функции выбора по ее значениям для двухэлементных и одноэлементных предъявлений

1. Фиксируем некоторое предъявление Х, для которого необходимо узнать результат выбора.
2. Фиксируем некоторый вариант у из этого предъявления, имея в виду проверить, выбирается или не выбирается вариант у из рассматриваемого предъявления.
3. Составляем все возможные двухэлементные подмножества {y,z} предъявления Х , содержащие вариант у .
4. ЕСЛИ y ∈ C({z,y}), (∀z ∈ X) , ТО y ∈ C(X), ИНАЧЕ y /∈ C(X).
5. Повторяем пп. 2-5 для других вариантов у.
6. Повторяем пп. 1-6 для других предъявлений Х.

Пример (при одноэлементном предъявлении выбор не пуст):

Подобные вычисления можно упростить, если их представить в виде следующей таблицы (матрицы):

Матрица отношения (таблица, упрощающая вычисления)

Порядок вычисления:

1. По предъявлению выделить часть матрицы

2. В выбор включаются те варианты, которым соответствуют строки подтаблицы, целиком заполненные единицами.