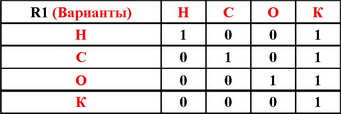
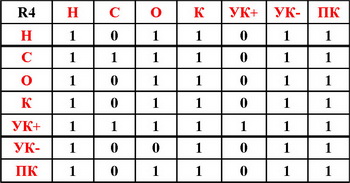
Принцип Кондорсе, эквивалентен выполнению и прямого , и обратного условий Кондорсе.
Функции выбора, удовлетворяющие принципу Кондорсе, называются нормальными.
Выполнение принципа Кондорсе эквивалентно одновременному выполнению свойств наследования и согласия. Функции с подобными свойствами исследуются в классической теории принятия решений.
Если выполняется принцип Кондорсе, то функция выбора однозначно определяется своими значениями для двух- и одноэлементных предъявлений.
Правило Кондорсе:
В выбор включаются те варианты, которые выигрывают все парные сравнения с другими вариантами и выбираются при одноэлементном предъявлении
Правило Парето :
В выбор включаются те варианты, которые выбираются при одноэлементном предъявлении и не имеют ни одного другого варианта, выигрывающего парное сравнение с данным вариантом (то есть не выбирающегося из соответствующего двухэлементного предъявления)
Нормальная функция выбора однозначно определяется своими значениями для двух- и одноэлементных предъявлений.
1. Фиксируем некоторое предъявление Х, для которого необходимо узнать результат выбора.
2. Фиксируем некоторый вариант у из этого предъявления, имея в виду проверить, выбирается или не выбирается вариант у из рассматриваемого предъявления.
3. Составляем все возможные двухэлементные подмножества {y,z} предъявления Х , содержащие вариант у .
4. ЕСЛИ y ∈ C({z,y}), (∀z ∈ X) , ТО y ∈ C(X), ИНАЧЕ y /∈ C(X).
5. Повторяем пп. 2-5 для других вариантов у.
6. Повторяем пп. 1-6 для других предъявлений Х.
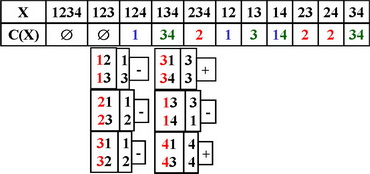
Подобные вычисления можно упростить, если их представить в виде следующей таблицы (матрицы):
| Варианты | 1. | 2. | 3. | 4. |
| 1. | 1 | 1 | 0 | 1 |
| 2. | 0 | 1 | 1 | 1 |
| 3. | 1 | 0 | 1 | 1 |
| 4. | 1 | 0 | 1 | 1 |

Порядок вычисления:
1. По предъявлению выделить часть матрицы
2. В выбор включаются те варианты, которым соответствуют строки подтаблицы, целиком заполненные единицами.
Принятие решений основывается на некотором исходном множестве возможных вариантов (G), из которого формируются предъявления (Х).
Механизм выбора состоит из структуры, заданной на исходном множестве (G), и правила выбора подходящих вариантов из предъявления (Х).
Структура позволяет произвести сравнение вариантов с целью их дальнейшего отбора по определенному правилу.
В зависимости от вида структуры механизм выбора может быть количественным или качественным.
Примером структуры является некоторый критерий, ставящий в соответствие каждому варианту некоторое число (функцию полезности).
Правило выбора может заключаться, например, в отыскании вариантов с наименьшим (наибольшим) значением критерия.
| Вариант | a | b | c | d | e |
| Критерий | 5 | 7 | 5 | 6 | 8 |
Критерий считается количественным, если его значения можно сравнивать по величине, указывая, на сколько или во сколько раз одно значение больше другого .
Качественные механизмы выбора используют структуры в виде отношений или качественных критериев,значения которых не имеет смысла сравнивать по величине.
Отношения отображают результаты попарных сравнений вариантов.
Эти результаты могут иметь разный смысл: например, при предъявлении двух вариантов {a} и {b} - вариант {а} "лучше" ("хуже", "не лучше", "не хуже", "предпочтительнее" , "несравним с" и т.п.) варианта {b}.
Не всякое отношение может быть выражено с помощью какого-либо критерия, но всякий количественный критерий может быть заменен соответствующим бинарным отношением.
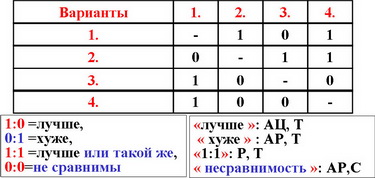
Отношение - это теоретико-множественное понятие, позволяющее дать качественное описание структуры на множестве вариантов.
Декартово (прямое) произведение множеств: Z :
X - 1-e исходное множество (состоит из элементов xi )
Y - 2-е исходное множество (состоит из элементов yj )
Z = X ⊗ Y - множество всех упорядоченных пар [ xi , yj ]
Пример :
X = { a, b, c} , Y = {1 ,2};
X ⊗ Y = {[a,1], [a,2], [b,1], [b,2], [c,1], [c,2]}.
Отношением R называется некоторое подмножество декартового произведения множеств: R ⊂ Z .
Например : R = {a1, c2, a2}. Это двухместное отношение.

Домен - некоторое именованное множество (часть предметной области), содержащее возможные значения простого свойства описываемых объектов (предметов, сущностей, связей ...). ( ® - MLT )
Атрибут - именованное простое свойство объекта, которое в конкретной ситуации принимает конкретное значение, принадлежащее соответствующему домену. ( ® - MLT )
Бинарное отношение – это двухместное отношение, в определении которого используется декартов квадрат, то есть Z = X ⊗ X ( Y = X) .
Многократное декартово произведение Z = X1 ⊗ X2 ⊗ X3 ⊗ . . . ⊗ Xn-1 ⊗ Xn .
Многоместным отношением R называется некоторое подмножество многократного декартового произведения множеств: R ⊂ Z .
z = [x1, x2, x3, . . . , xn-1, xn] - кортеж = « n – ка » :
[a,1,x] – тройка, [a,1,x,M] – четверка, [y,3] – пара.
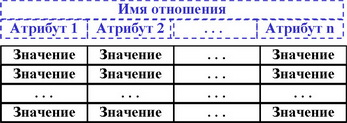
Схема отношения : R (атрибут, атрибут, ..., атрибут)
Пример : Расписание (№ рейса, п.н., Т отпр. )
А. - правилом, (например, многоугольники, имеющие одинаковые цвет и число вершин),
Б. - перечислением, (например, {1,2} {1,4} {2,5} ...),
В. - таблицей (табличное представление),
Г. - матрицей отношения, (см. таблицу попарных сравнений)
Д. - графом (для бинарных отношений).
Табличное представление отношения содержит все входящие в него кортежи, упорядоченные по строкам.
Упорядочение по столбцам определяется схемой отношения, т.е. столбцы связываются с атрибутами.
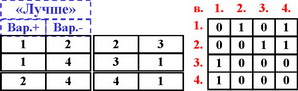
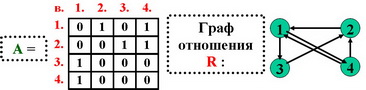
Бинарное отношение R позволяет выразить результаты попарных сравнений вариантов с помощью множества пар вида [x, y]: {[1,2],[1,4],[2.3],[2,4],[3,1],[4,1]}, причем, на первом месте указывается номер выбираемого варианта из данной пары.
В матрице (A) отношения R эти результаты выражаются единичными элементами ai,j =1 на пересечении соответствующих строк и столбцов.
1. Максимальное число мест отношений совпадает с числом вариантов.
2. Выбираемому варианту необходимо поставить в соответствие первый атрибут.
3. Невыбираемым вариантам ставятся в соответствие остальные (пассивные) атрибуты.
4. Для сокращения избыточности пассивные атрибуты наделяются дополнительным свойством – перестановочности.

Множество X: X = {Н,С,О,НС,НО,СО,НСО,К,УК+,УК-,ПК}
Декартово произведение: X ⊗ X R ⊂ X ⊗ X
Отношения: R1 = «необходимость» R2 = «достаточность» R3 = «НиД» X = {Н,С,О, К}