Декартово (прямое) произведение множеств: Z :
X - 1-e исходное множество (состоит из элементов xi )
Y - 2-е исходное множество (состоит из элементов yj )
Z = X ⊗ Y - множество всех упорядоченных пар [ xi , yj ]
Пример :
X = { a, b, c} , Y = {1 ,2};
X ⊗ Y = {[a,1], [a,2], [b,1], [b,2], [c,1], [c,2]}.
Отношением R называется некоторое подмножество декартового произведения множеств: R ⊂ Z .
Например : R = {a1, c2, a2}. Это двухместное отношение.

Домен - некоторое именованное множество (часть предметной области), содержащее возможные значения простого свойства описываемых объектов (предметов, сущностей, связей ...). ( ® - MLT )
Атрибут - именованное простое свойство объекта, которое в конкретной ситуации принимает конкретное значение, принадлежащее соответствующему домену. ( ® - MLT )
Бинарное отношение – это двухместное отношение, в определении которого используется декартов квадрат, то есть Z = X ⊗ X ( Y = X) .
Многократное декартово произведение Z = X1 ⊗ X2 ⊗ X3 ⊗ . . . ⊗ Xn-1 ⊗ Xn .
Многоместным отношением R называется некоторое подмножество многократного декартового произведения множеств: R ⊂ Z .
z = [x1, x2, x3, . . . , xn-1, xn] - кортеж = « n – ка » :
[a,1,x] – тройка, [a,1,x,M] – четверка, [y,3] – пара.
Схема отношения : R (атрибут, атрибут, ..., атрибут)
Пример : Расписание (№ рейса, п.н., Т отпр. )
А. - правилом, (например, многоугольники, имеющие одинаковые цвет и число вершин),
Б. - перечислением, (например, {1,2} {1,4} {2,5} ...),
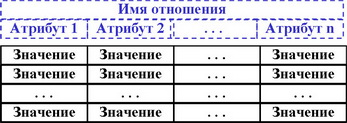
В. - таблицей (табличное представление),
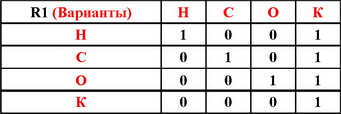
Г. - матрицей отношения, (см. таблицу попарных сравнений)
Д. - графом (для бинарных отношений).
Табличное представление отношения содержит все входящие в него кортежи, упорядоченные по строкам.
Упорядочение по столбцам определяется схемой отношения, т.е. столбцы связываются с атрибутами.
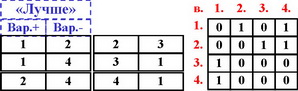
Бинарное отношение R позволяет выразить результаты попарных сравнений вариантов с помощью множества пар вида [x, y]: {[1,2],[1,4],[2.3],[2,4],[3,1],[4,1]}, причем, на первом месте указывается номер выбираемого варианта из данной пары.
В матрице (A) отношения R эти результаты выражаются единичными элементами ai,j =1 на пересечении соответствующих строк и столбцов.
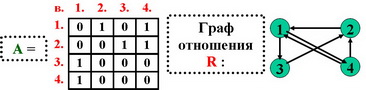
1. Максимальное число мест отношений совпадает с числом вариантов.
2. Выбираемому варианту необходимо поставить в соответствие первый атрибут.
3. Невыбираемым вариантам ставятся в соответствие остальные (пассивные) атрибуты.
4. Для сокращения избыточности пассивные атрибуты наделяются дополнительным свойством – перестановочности.

Вырожденные случаи отношений: пустое = ∅ и полное = 1. Пусть заданы два отношения R1 и R2.
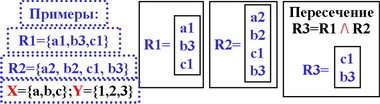
Пересечение отношений R3=R1 /\ R2= ?
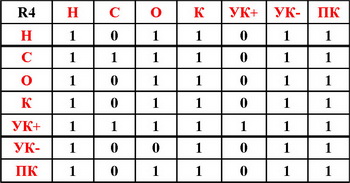
Объединение отношений R4=R1 \/ R2= ?
Дополнение отношений R5 = ?
Вычитание отношений R6=R1 / R2, R7=R2/R1=?
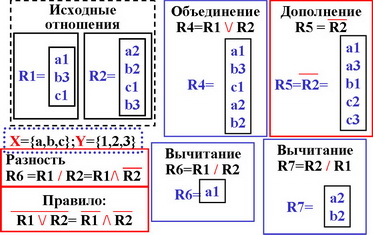
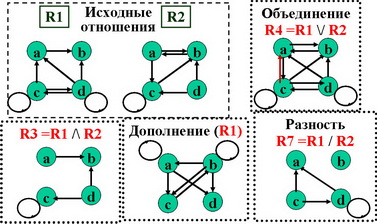
Определяется по аналогии с декартовым произведением множеств, учитывая особенности отношений, как множеств специального вида.
Важнейшей особенностью отношения является наличие схемы.
Конкатенация элементов, записей и схемы.
Пример.
R8=R1 ⊗ R2= ?
где R1={a1,b3,c1}, R2={a2, b2, c1, b3}
R8 = {a1a2, a1b2, a1c1, a1b3, b3a2, b3b2, b3c1, b3b3, c1a2, c1b2, c1c1, c1b3}
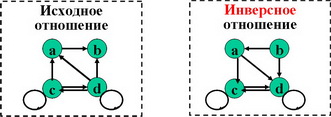
Операцию инверсии отношений можно трактовать как переименование атрибутов: атрибуты отношения меняются местами, хотя записи не изменяются, т.е. столбцы таблицы отношения остаются на месте:

При инвертировании бинарного отношения его матрица транспонируется: M2 = (M1)т
На графе бинарного отношения следует изменить на противоположное направление всех связей.
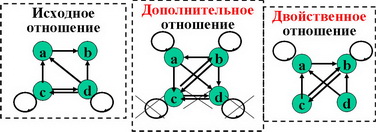
Двойственное отношение это дополнение инверсного отношения.
Матрица транспонируется, 1=> 0, 0=>1 .
Петли и кольца – удаляются, но вставляются отсутствующие петли и кольца.
Простые дуги - остаются без изменения
Множество X: X = {Н,С,О,НС,НО,СО,НСО,К,УК+,УК-,ПК}
Декартово произведение: X ⊗ X R ⊂ X ⊗ X
Отношения: R1 = «необходимость» R2 = «достаточность» R3 = «НиД» X = {Н,С,О, К}