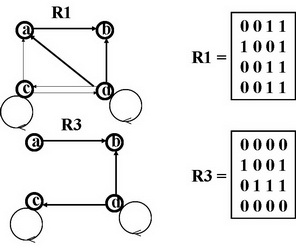
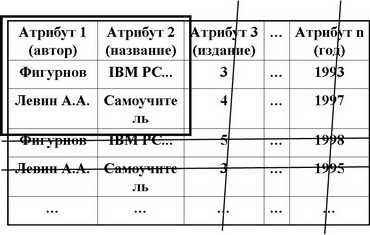
Проекции используются для разделения отношений на более простые части, нужные в данный момент пользователю, либо при соединении которых можно будет полностью восстановить всю информацию.
При описании операции проекции используется множество удаляемых атрибутов.
В схеме результирующего отношения сохраняются только заданные атрибуты, оставшиеся после удаления атрибутов, значения которых не интересны для пользователя.
Таблица результирующего отношения получается из таблицы исходного отношения вычеркиванием столбцов, соответствующих удаленным атрибутам, с последующим устранением повторяющихся записей.
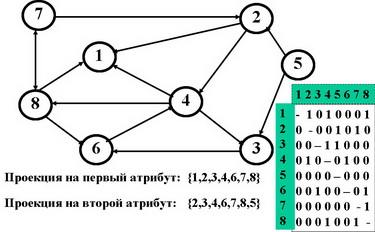
Дуги: {[1,2],[1,4],[1,8],[2,5],[2,7],[3,4],[3,5],[4,2],[4,6],[6,3],[6,8],[7,8],[8,7],[8,4]}
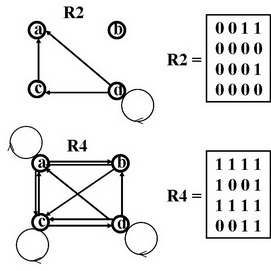
Эта операция позволяет собрать сложное отношение из более простых частей, и во многих случаях восстановить всю имеющуюся в них информацию.
При описании операции соединения используется множество соединяемых атрибутов.
В схемах всех исходных отношений соединяемые атрибуты должны обязательно присутствовать.
В схеме результирующего отношения указываются все атрибуты исходных отношений, но соединяемые атрибуты не дублируются.
Таблица результирующего отношения получается из таблиц исходных отношений путем сбора всех записей, с одинаковыми значениями соединяемых атрибутов.

Экви-соединение является таким обобщением простого соединения , когда не требуется обязательного совпадения соединяемых атрибутов разных отношений, но их значения связаны некоторым отношением эквивалентности.
Например, последовательное соединение двух устройств, предусматривает подачу выхода первого устройства на вход второго.
Второй пример, сопряжение двух региональных расписаний, в которых имеются общие промежуточные пункты. Такие атрибуты как «время прибытия» и «время отправления» легко пересчитываются при известном времени стоянки и поэтому связаны отношением эквивалентности.
Тэта-соединение является дальнейшим обобщением простого соединения, когда значения соединяемых атрибутов разных отношений связаны произвольным отношением, обозначаемым греческой буквой тэта.
Характерный пример – задача планирования поездки через пересадочный пункт на основе двух региональных расписаний, содержащих этот пункт. Здесь значения атрибутов «время прибытия в пункт пересадки» и «время отправления из пункта пересадки» связаны отношением «раньше».
Схема результирующего отношения при тэта-соединении и экви-соединении сохраняет все атрибуты исходных отношений, несмотря даже на возможность дублирования значений.
Композиция отношений выполняется путем последовательного обращения к двум операциям: соединения, и проекции на несоединяемые атрибуты.
Например, при последовательном соединении устройств, пользователи всего агрегата обычно не интересуются промежуточными сигналами соединяемых устройств.
Вторым характерным примером является задача планирования поездки через пересадочный пункт когда пассажира не интересуют значения атрибутов «время прибытия в пункт пересадки» и «время отправления из пункта пересадки» , а важно лишь время прибытия в пункт назначения.
Пусть известны схемы исходных отношений
R1(A,A1,A2, ... An-1), (n – местное)
R2(A,B1,B2, ... Bm-1), (m – местное)
Какова будет схема результирующего отношения?
R(A1,A2, ... An-1 , B1,B2, ... Bm-1).
Число мест результирующего отношения:
n + m - 2
Композиция произвольного отношения с двухместным не изменяет количества мест результирующего отношения.
Что получается при композиции двух бинарных отношений?
Результатом композиции бинарных отношений является снова бинарное отношение.
Оба отношения должны быть определены на одном и том же множестве, являющемся доменом для всех атрибутов.
В зависимости от соединяемых атрибутов возможны 4 варианта выполнения композиции, выражаемые через инверсию того или иного отношения.

Операция композиции бинарных отношений считается стандартной, если в соединение входят второй атрибут первого отношения и первый атрибут второго отношения.
Композиция отношения с самим собой называется квадратом бинарного отношения.
Композиция квадрата бинарного отношения с исходным отношением называется кубом исходного отношения.
Аналогично может быть определена любая степень бинарного отношения.
На графе отношения его степень интерпретируется как граф маршрутов, длина которых равна показателю степени.
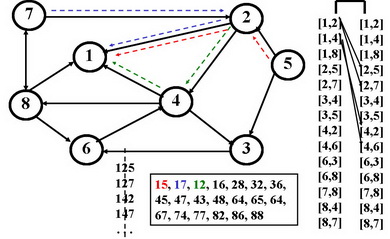
Матрица композиции двух отношений равна логическому произведению матриц исходных отношений.
Матрицы бинарных отношений состоят из логических элементов (1,0) и поэтому должны перемножаться с использованием логических операций сложения (ИЛИ) и умножения (И).
В математических пакетах матрицы обычно перемножаются арифметически , что дает дополнительную информацию не только о наличии требуемого маршрута, но и о количестве таких маршрутов.
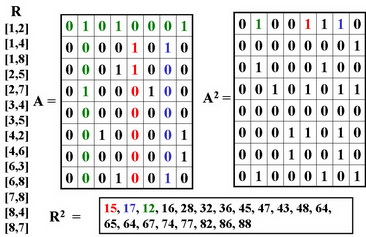
"Всякое многоместное отношение может быть представлено в виде композиции конечного числа трехместных отношений"
Композиция двухместного отношения с произвольным отношением не изменяет количества мест последнего.
Пусть R=R(A1,A2,A3, ..., An).
Введем фиктивный атрибут Х со значениями, равными номеру строки табличного представления R.
Заменим 2 первых столбца (А1,А2) табличного представления R столбцом Х. Получим отношение R1=R1(X,A3,A4,...An).
Сама замена описывается отношением R2=R2(A1,A2,X). (Это трехместное отношение!)
Так как атрибут X отношения R1(X,A3,A4, ... , An) является ключевым для отношения R, то композиция R1 и R2(A1,A2,X) полностью и точно восстановит исходное отношение.
В то же время количество мест отношения R1 уменьшилось на 1 по сравнению с отношением R.
Теперь можно применить тот же самый прием к отношению R1=R1(X,A3,A4, ... , An) и еще уменьшить число атрибутов.
Повторяя предыдущий шаг к отношению R1, получим через конечное число шагов композицию, о которой говорится в теореме.
Горизонтальным сечением ( Rx ) бинарного отношения R называется множество значений второго атрибута, входящие во все кортежи отношения, в которых первый атрибут равен x.
Горизонтальное сечение можно найти, выбрав те кортежи, в который первый атрибут равен x, и сделав проекцию на второй атрибут.
Так как выбор кортежей, в которых первый атрибут равен х, - это операция соединения (по первому атрибуту) исходного отношения с унарным отношением {x}, то Rx является композицией R и {x}
Горизонтальное сечение часто называют левым сечением (по месту расположения фиксированного атрибута).
Вертикальным сечением ( Ry ) бинарного отношения R называется множество значений первого атрибута, входящие во все кортежи отношения, в которых второй атрибут равен y.
Вертикальное сечение можно найти, выбрав те кортежи, в который второй атрибут равен y, и сделав проекцию на первый атрибут.
Так как выбор кортежей, в которых второй атрибут равен y, - это операция соединения (по второму атрибуту) исходного отношения с унарным отношением {y}, то Ry является композицией R и {y}
Вертикальное сечение часто называют правым сечением (по месту расположения фиксированного атрибута).
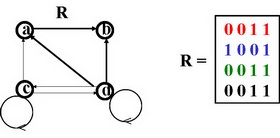
Горизонтальные сечения (ГС( )) :
ГС(a) = {c, d }; ГС(b) = {a, d }; ГС(c) = {c, d }.
Вертикальные сечения (ВС( )) :
ВС(a) = {b}; ВС(c) = {b}; ВС(d) = {a,b,c,d}.
Сечением ( Ry ) n-местного отношения R называется (n-1)-местное отношение, являющееся композицией R и {y} по заданному атрибуту, значение которого зафиксировано величиной y.
Разрез можно найти, выбрав те кортежи, в который заданный атрибут равен y, и сделав проекцию на остальные атрибуты.
Так вертикальное сечение отношения R является разрезом бинарного отношения по второму атрибуту.
При построении разреза информация, имеющаяся в отношении, не теряется (кроме значения фиксированного атрибута), которое можно сохранить в имени разреза.
Максимумом бинарного отношения R называется такой элемент y1 исходного множества, в горизонтальное сечение которого входят все элементы исходного множества.
Минорантой бинарного отношения R называется такой элемент y0 исходного множества, горизонтальное сечение которого пусто.
Если R играет роль отношения предпочтения, то максимумами являются те варианты, которые лучше других или , по крайней мере не уступают другим.
Миноранты или хуже других вариантов, или такие же как они.
Минимумом бинарного отношения R называется такой элемент z1 исходного множества, в вертикальное сечение которого входят все элементы исходного множества.
Мажорантой бинарного отношения R называется такой элемент z0 исходного множества, вертикальное сечение которого пусто.
Если R играет роль отношения строгого предпочтения, то мажорантами являются те элементы, которые не имеют превосходящих их вариантов.
Минимумы или хуже других вариантов, или такие же как они.