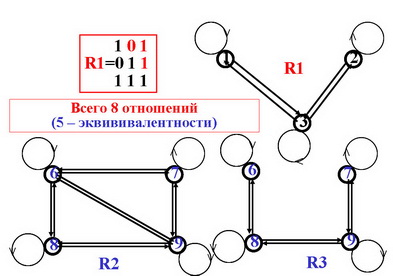
Отношение R называется транзитивным, если всегда, когда две пары (х, у) и (у,z) входят в R, то и пара (х,z) тоже входит в R.
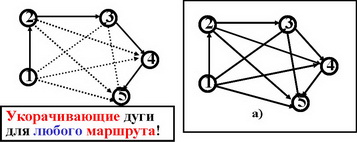
Если отношение R содержит кольца, то у студентов могут возникнуть типичные ошибки:
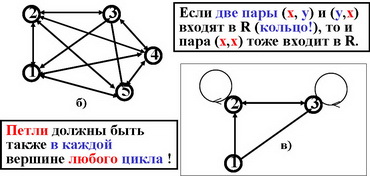
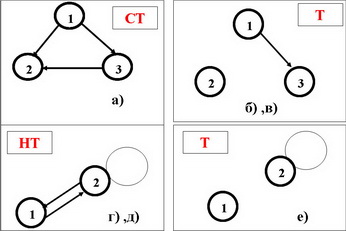
1. Операции инверсии и пересечения транзитивных отношений сохраняют их свойство транзитивности (Т).
2. Добавление к графу транзитивного отношения петель не изменит свойства Т этих отношений.
3. Возведение в квадрат транзитивного отношения не приводит к появлению новых пар : R2 ⊆ R.
4. Возведение транзитивного отношения в любую степень не приводит к появлению новых пар : Rk ⊆ R.
5. Свойство 3 является необходимым и достаточным условием транзитивности отношения R .
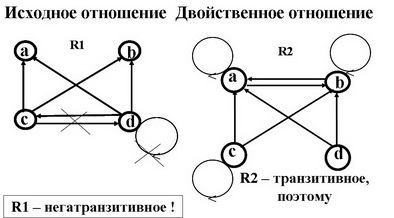
Отношение R называется негатранзитивным, если отсутствие дуг от х к у и от у к z приводит к отсутствию дуги от х к z .
Двойственность свойств транзитивности и негатранзитивности:
Отношение R является негатранзитивным, если его дополнение Rдоп транзитивно и наоборот.
Если из графа негатранзитивного отношения удалять петли, то свойство негатранзитивности сохранится.
В графе негатранзитивного отношения отсутствие связи (кольца или дуги) между двумя вершинами влечет отсутствие петель в обоих вершинах.
Отношение R называется сильно транзитивным , если оно одновременно транзитивно и негатранзитивно.
Если отношение R является сильнотранзитивным, то его дополнение Rдоп сильнотранзитивно и наоборот.
При переходе к инверсному или двойственному отношению свойство сильной транзитивности также сохраняется.
В графе сильнотранзитивного отношения отсутствие связи (кольца или дуги) между двумя вершинами влечет отсутствие петель в обоих вершинах, но, если есть кольцо, то должны быть и петли.
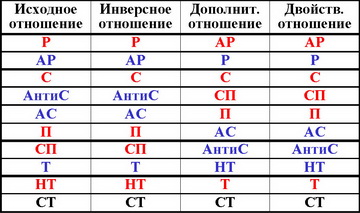
Два свойства называются двойственными друг к другу, если выполнение одного из них для исходного отношения является необходимым и достаточным условием выполнения другого для двойственного отношения.
Как изменяются свойства при переходе к инверсному, дополнительному и двойственному отношениям?
Двойственное утверждение, получается из уже известного утверждения заменой исходных понятий и свойств соответствующими двойственными понятиями и свойствами. Найдите двойственные утверждения в лекции №11!
Если справедливо некоторое утверждение относительно исходных понятий, то справедливо и двойственное утверждение, получаемое заменой исходных понятий и свойств соответствующими двойственными понятиями и свойствами.
Пример.
Исходное утверждение:
7. Транзитивное, антирефлексивное и слабосвязное бинарное отношение R всегда сильно транзитивно.
Двойственное утверждение:
7’. Негатранзитивное, рефлексивное и антисимметричное бинарное отношение R всегда сильно транзитивно.
1. Асимметричная и симметричная части транзитивного отношения транзитивны.
Маршрут, проходящий через простые дуги графа транзитивного отношения, может укорачиваться только через простую дугу.
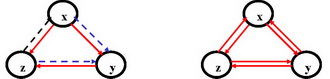
Маршрут, проходящий через кольца графа транзитивного отношения, может укорачиваться только через кольцо.
2. Антирефлексивное и транзитивное бинарное отношение R всегда ациклично.
Из предположения наличия цикла в условиях транзитивности отношения придем выводу о наличии петель в каждой вершине, через которые проходит цикл. Но петли противоречат условию антирефлексивности.
3. Асимметричное и транзитивное бинарное отношение R всегда ациклично.
Это утверждение является следствием утверждения 2, так как асимметричное отношение обязательно является антирефлексивныи.
4. Негатранзитивное и асимметричное бинарное отношение R всегда транзитивно.
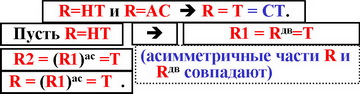
5. Транзитивное и полносвязное бинарное отношение R всегда негатранзитивно.
Для доказательства надо применить принцип двойственности к утверждению 4.
6. Ацикличное и слабосвязное бинарное отношение R всегда сильно транзитивно.
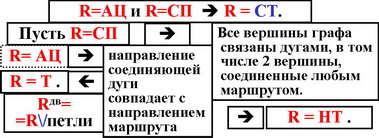
7. Транзитивное, антирефлексивное и слабосвязное бинарное отношение R всегда сильно транзитивно. (Следствие 6. и 2.)
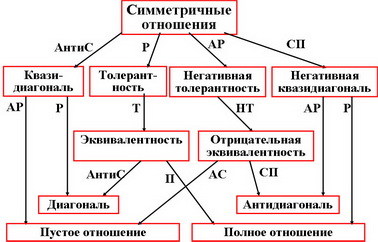
Бинарное отношение R называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно (1).
Примеры:
отношение подобия на множестве треугольников;
отношение равенства чисел по модулю n;
отношения типа "быть коллегой или быть сокурсником".(Лингвистическая проблема)
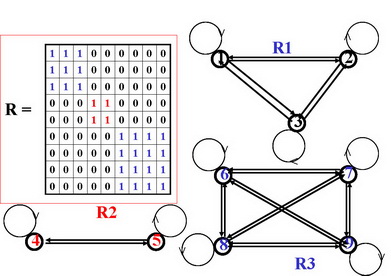
Задание отношения эквивалентности на некотором множестве означает разбиение этого множества на непересекающиеся подмножества (классы) эквивалентных друг другу элементов и наоборот, любое разбиение множества на непересекающие классы определяет соответствующую этому разбиению эквивалентность.
Если предъявление включает варианты только из одного класса эквивалентности, то выбирается все предъявление (жадный выбор).
Если предъявление включает варианты из разных классов эквивалентности, то происходит отказ от выбора (пустой выбор).

Отношение толерантности (безразличия) определяется наличием свойств рефлексивности и симметричности (2).
Примеры:
1. Отношение «иметь хотя бы одного общего родителя».
2. Отношение «соседние или равные целые числа».
3. Расширенное отношение «быть соседом».
4. Отношение толерантности между тремя вариантами x, y, z , когда вариант z всегда предпочтительнее других, может возникнуть в одном из следующих трех случаях:
- эксперт считает, что нет разницы между вариантами х и у;
- эксперт не уверен в строгом превосходстве одного варианта над другим;
- эксперт считает варианты х и у несравнимыми между собой.
1. Отношение эквивалентности является частным случаем отношения толерантности, а именно транзитивным отношением толерантности.
2. При объединении отношений эквивалентности всегда получается отношение толерантности.
3. Любое отношение толерантности можно представить в виде объединения некоторых отношений эквивалентности.
3.1. Выделить диагональ
3.2. Выбрать кольцо и составить «2-эквивалент»
3.2.1. Включить в него это кольцо
3.2.2. Удалить варианты, связанные кольцом
3.2.3. Включить в «2-эквивалент» любое оставшееся кольцо. И т.д. Объединить все с диагональю.
3.3. И т.д.