
Свойства многокритериальных механизмов могут быть выражены двумя способами:
а) в пространстве вариантов,
б) в пространстве критериев.
В одну и ту же точку пространства критериев могут отображаться несколько точек пространства вариантов. Такие варианты назовем критериально эквивалентными. Любой из них можно заменить эквивалентным представителем.
Если все результаты выбора отображаются в одну и ту же точку критериального пространства, то такое решение будем называть критериально-единственным.
По аналогии и в других случаях слово «критериально» указывает на рассмотрение свойств вариантов в критериальном пространстве.
Все многокритериальные (векторные) механизмы выбора определяются либо через механизм попарных предпочтений (МВНР), либо через механизм попарных блокировок (Парето). Поэтому порождаются нормальные функции выбора, т.е. свойства Н и С - выполнены.
Механизм выбора наилучших решений (МВНР) часто не дает результата (отказ от выбора, выбор пуст), а если выбор не пуст, то его решения оказываются критериально единственными.
Механизмы Парето и Слейтера ( при конечном числе вариантов) всегда приводят к непустому выбору. (Ацикличность отношений).
Координатные отношения, используемые в этих механизмах, являются транзитивными, поэтому выполнено свойство О
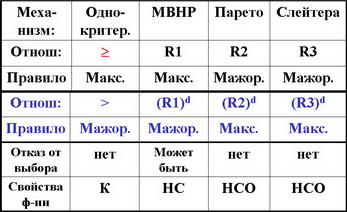
Если выбор не пуст, то наилучшее решение (по МВНР) удовлетворяет свойству критериальной единственности.
Если эффективное решение (решение Парето) удовлетворяет свойству критериальной единственности, то оно является наилучшим (МВНР).
Если слабоэффективное решение (решение Слейтера) удовлетворяет свойству критериальной единственности, то оно является наилучшим (МВНР), (и решением Парето) .
Всякое эффективное решение (решение Парето) является также и слабоэффективным (решением Слейтера). ( Множество проверок Слейтера не шире множества проверок Парето).
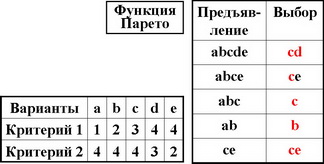
Наилучшее решение (МВНР) не существует тогда и только тогда, когда функция Парето в критериальном пространстве дает неединственное решение. В этом случае свойство К не выполняется.
Если свойство К выполняется, то функция многокритериального выбора может быть скаляризована, т.е. сведена к однокритериальной.
Любой механизм выбора определяется структурой и правилом.
Структура многокритериальных механизмов выбора задается таблицами значений критериев в зависимости от рассматриваемого варианта.
Правило многокритериального механизма выбора основывается на попарных сравнениях векторных оценок вариантов аналогично бинарным механизмам выбора.
То есть многокритериальные механизмы выбора можно рассматривать как частные случаи бинарных механизмов выбора, в которых в качестве структуры используются те или иные координатные отношения.
1. Механизм векторного предпочтения является пересечением механизмов однокритериального предпочтения. (Возможен отказ от выбора, НСО)
2. Механизм Парето является частным случаем механизма блокировок , в котором используется отношение Парето, построенное по таблицами значений критериев. (Непустой выбор, НСО)
3. Механизм Слейтера является частным случаем механизма блокировок , в котором используется отношение Слейтера, построенное по таблицами значений критериев. (Непустой выбор, НСО)
Отношения Парето и Слейтера являются частными случаями качественных порядков (свойства ацикличности и транзитивности). Вообще то для каждой конкретной задачи они отличаются друг от друга, при том, что отношение Слейтера является частью отношения Парето.
Множества отношений Слейтера и Парето являются подмножествами отношений качественного порядка.
Выявление связей (или отличий) между ними позволяет уточнить свойства механизмов Парето и Слейтера (Непустой выбор, НСО)
Построение отношения Парето или Слейтера означает нахождение таблицы значений критериев для соответствующего многокритериального механизма.
Результаты сравнения множеств механизмов:
а), б) Механизмы одного типа сводятся к механизмам другого типа;
в) Множества механизмов эквивалентны,
г), д) Множества механизмов пересекаются или не пересекаются.
Задано отношение качественного порядка, используемое в механизме попарных блокировок.
Требуется определить компоненты векторного критерия для механизма Парето, дающего тот же самый результат.
Из предыдущего материала известно, что функция Парето обладает свойствами: непустой выбор, Н, С, О.
Положительное решение поставленной задачи для любого качественного порядка доказывает обратное утверждение:
Для всякой функции непустого выбора со свойствами Н, С, О может быть подобран механизм Парето, дающий тот же самый результат.
1. Составим матрицу отношения, проверим свойства качественного порядка.
2. На месте единичных элементов запишем значение, равное двум.
3. На месте диагональных элементов запишем значение, равное единице.
4. Каждый столбец полученной матрицы рассматриваем как один из критериев многокритериального механизма.
Чему равно число критериев полученного механизма Парето?
Если в исходном отношении связи между вариантами нет, то может ли она появиться в отношении Парето?
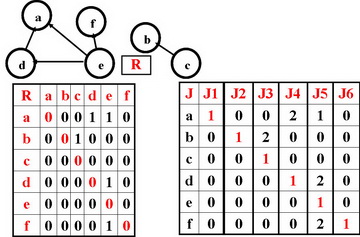
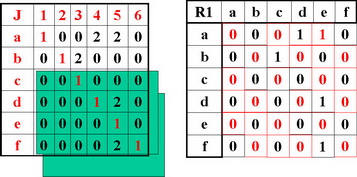
Возьмем произвольные 3 варианта x, y, z и три соответствующие им компоненты векторного критерия f1(t) = Jx(t), f2(t) = Jy(t), f3(t) = Jz(t).
Если по исходному отношению вариант x лучше варианта y, то f1(y) = 2 (по построению) и остается показать, что все значения критерия f1(t) не меньше соответствующих значений f2(t): f1(t) >= f2(t).
Это так, поскольку:
1. f1(x) = 1 (по построению), а f2(x) = 0 (по предположению),
2. (в силу произвольности z) f1(z) >= f2(z), (если f2(z) = 2 (т.е. y лучше чем z), то в силу транзитивности исходного отношения имеем x лучше чем z, значит (по построению) f1(z) = 2.

Задано отношение качественного порядка, используемое в механизме попарных блокировок.
Требуется определить компоненты векторного критерия для механизма Слейтера, дающего тот же самый результат.
Из предыдущего материала известно, что функция Слейтера обладает свойствами: непустой выбор, Н, С, О.
Положительное решение поставленной задачи для любого качественного порядка доказывает обратное утверждение:
Для всякой функции непустого выбора со свойствами Н, С, О может быть подобран механизм Слейтера, дающий тот же самый результат.
(Число критериев равно числу вариантов)
0. Каждому варианту ставится в соответствие своей критерий, упорядочивающий все варианты относительно рассматриваемого варианта.
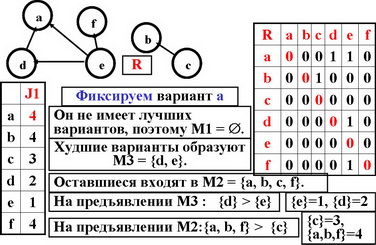
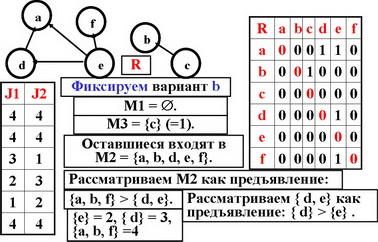
1. Выберем некоторый вариант х.
2. Разобьем множество выбора на три множества (М1,М2,М3), причем М1 содержит варианты лучшие, чем х, а М3 – худшие чем х .
3. Рассматривая подмножества каждого из этих множеств как предъявления, упорядочим (последовательным отбором) множества и их подмножества.
4. Пронумеруем все эти подмножества в направлении возрастания предпочтительности. Значение критерия для любого варианта равно номеру подмножества, в которое он входит.
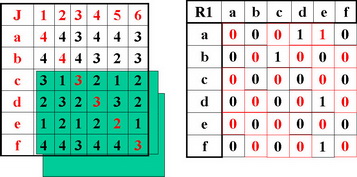
Возьмем произвольные 3 варианта x, y, z и три соответствующие им компоненты векторного критерия f1(t) = Jx(t), f2(t) = Jy(t), f3(t) = Jz(t).
Если по исходному отношению вариант x лучше варианта y, то f1(y) = 2 (по построению) и остается показать, что все значения критерия f1(t) не меньше соответствующих значений f2(t): f1(t) >= f2(t).
Это так, поскольку:
1. f1(x) = 1 (по построению), а f2(x) = 0 (по предположению),
2. (в силу произвольности z) f1(z) >= f2(z), (если f2(z) = 2 (т.е. y лучше чем z), то в силу транзитивности исходного отношения имеем x лучше чем z, значит (по построению) f1(z) = 2.

Если имеется механизм Слейтера, то по нему составляется отношение Слейтера, которое является качественным порядком.
Преобразуем этот качественный порядок в таблицу критериев механизма Парето.
Если имеется механизм Парето, то по нему составляется отношение Парето, которое является качественным порядком.
Преобразуем этот качественный порядок в таблицу критериев механизма Слейтера.
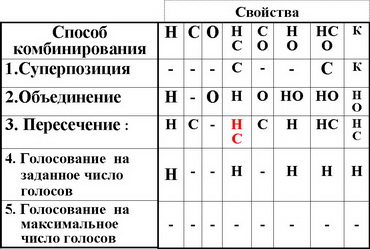
Суперпозиция:
1. Скалярно-скалярный механизм → К
2. Скалярно-векторный механизм → НСО
3. Векторно-скалярный механизм → С
4. Векторно-векторный механизм → С
Первое прилагательное характеризует механизм выбора, реализованный на первой (входной) ступени обработки предъявления.
